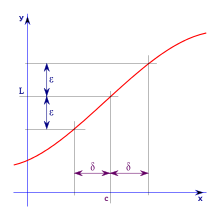
This section we will see upper and lower bounds of a a function.
We know that any number greater than or equal to all the elements of a set is called upper bound. For the interval [0, 1, 2, 3, 4, 5, 6], 6 can be an upper bound. Also, 1, 2, 3, 4, 5, 6 are upper bounds for this set.
A lower is a number which is less than or equal to all the elements of particular set. We can say that for a set [6, 7, 9], 6 be a lower bound.
For a set { 5, 11, 54, 139}, 5 could be a lower bound, but 9 is definitely not. Also, for the set {66}, 66 is lower and upper bound both. Other numbers would be either a lower or an upper bound for this set.
A lower is a number which is less than or equal to all the elements of particular set. We can say that for a set [6, 7, 9], 6 be a lower bound.
For a set { 5, 11, 54, 139}, 5 could be a lower bound, but 9 is definitely not. Also, for the set {66}, 66 is lower and upper bound both. Other numbers would be either a lower or an upper bound for this set.
A subset of natural numbers must have a lower bound, since natural numbers start from 1. But an infinite subset of natural numbers do not have upper bound. The infinite integer subset could be bounded from above or below, but not both. Similarly, for an infinite subset of rational numbers.